变换作图中的常用模板函数
前言
体会常用模板函数在变换作图中的重要性;提起函数图像的作图方法,估计好多学生会一口锁定描点法,其实高中更多使用的是变换作图法,尤其是在分秒必争的高考中。要想在很短的时间内,做出一个函数的大致草图,缺乏平时的对应训练几乎是不可能的。因此我们需要研究和总结函数图像的常用模板。
体会感悟
比如我们常常把函数\(f(x)=x+\cfrac{1}{x}\)作为模板,意思是对这个函数的大致图像我们要掌握的非常熟练。 那么我们为什么要把函数\(f(x)=x+\cfrac{1}{x}\)作为模板来看呢?
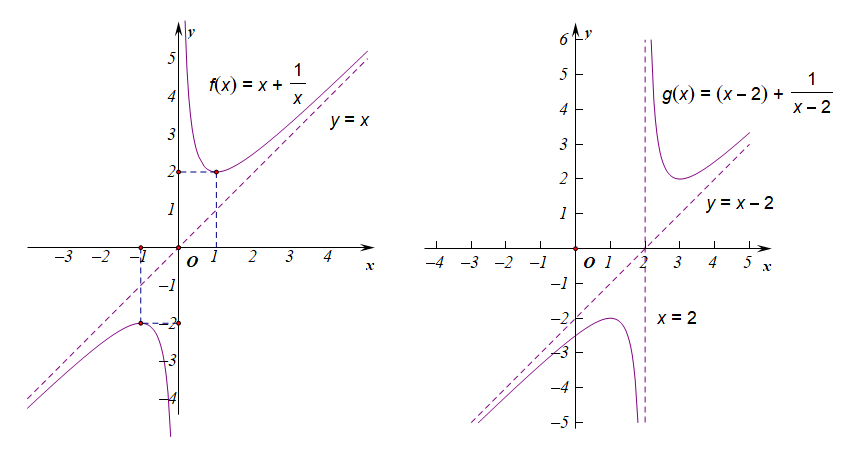
请大家先看一个函数\(h(x)=\cfrac{x^2-4x+5}{x-2}\),这个函数在高三数学学习中应该很常见,初次接触我们感觉很恐怖,心里都没有底,主要原因是不知道这个函数的图像和性质到底是什么样的。
别着急,慢慢看,我们对这个函数做个变换,
\(h(x)=\cfrac{x^2-4x+5}{x-2}=\cfrac{(x-2)^2+1}{x-2}=(x-2)+\cfrac{1}{x-2}\xrightarrow{x-2=t}t+\cfrac{1}{t}\),
看到变换最后的函数\(g(t)=t+\cfrac{1}{t}\),应该不陌生,看着眼熟吧,这时候你还害怕吗?对了,我们心里稍稍安稳了一些,通过模板函数的图像变换就可以搞定它,那你还害怕什么呢?
具体变换思路:先做出函数\(f(x)=x+\cfrac{1}{x}\),然后将函数\(f(x)\)的图像向右平移2个单位,得到函数\(f(x-2)\),
也就是函数\(f(x-2)=(x-2)+\cfrac{1}{x-2}=\cfrac{(x-2)^2+1}{x-2}=\cfrac{x^2-4x+5}{x-2}=h(x)\),不是很简单吗?如右图所示,当我们把模板函数的性质研究的透透的,对于函数\(h(x)\)的图像和性质不也就知道了吗?
- 比如给出的这些貌似恐怖的函数,通过变换我们都能找到它们的模板函数
\(f(x)=\cfrac{x^2+2x+2}{x+1}\);\(g(x)=\cfrac{x^2+2x}{x+1}\);\(m(x)=\cfrac{x^2+3x+3}{x+1}\);
\(n(x)=\cfrac{x+1}{x^2+3x+3}\);\(l(t)=\cfrac{1+t^2}{1+2\sqrt{2}t}\);\(h(x)=\cfrac{x^2-4x+5}{x-2}\);
模板函数
- 各种常见的基本初等函数自然都是模板函数,比如
- 重点掌握
\(f(x)=|2^x-1|\),\(g(x)=|\lg x|\)
研究方法
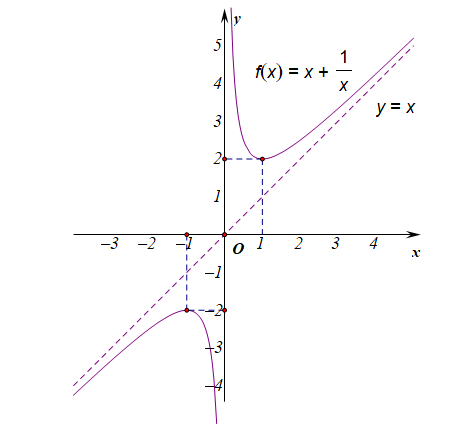
- 以函数\(y=x+\cfrac{1}{x}\)的单调性探究为案例,
定义域是\(x\in(-\infty,0)\cup(0,+\infty)\),且是奇函数,故只先研究\(x\in(0,+\infty)\)上的图像,研究工具是导数。
先求导,得到\(f'(x)=1-\cfrac{1}{x^2}=\cfrac{x^2-1}{x^2}\),
令\(f'(x)>0\),即\(x^2-1>0\),得到\(x>1\);
令\(f'(x)<0\),即\(x^2-1<0\),得到\(0<x<1\);结合奇函数的特性,
可知,函数在区间\((-\infty,-1]\)单增,在\([-1,0)\)单减,在\((0,1]\)单减,在区间\([1,+\infty)\)单增,又\(f(1)=2,f(-1)=-2\),
所以可以手动做出函数的图像如下:
-
函数\(y=ax+\cfrac{b}{x}(a,b>0)\)的单调性探究:仿照上例,自行探究。
-
函数\(y=x-\cfrac{k}{x}(k>0)\)的单调性探究:仿照上例,自行探究。
相关方法
变形时可能用到的主要方法有配凑法和换元法,我们知道,以下的这些变形其实都是以上述的函数为模板变换得到的
比如\(f(x)=\cfrac{x^2+2x+2}{x+1}\);\(g(x)=\cfrac{x^2+2x}{x+1}\);\(m(x)=\cfrac{x^2+3x+3}{x+1}\);\(n(x)=\cfrac{x+1}{x^2+3x+3}\);\(l(t)=\cfrac{1+t^2}{1+2\sqrt{2}t}\);\(h(x)=\cfrac{x^2-4x+5}{x-2}\);
变形时用到的主要方法:配凑法和换元法,如果容易配凑,则用配凑法,如果不容易配凑则使用换元法,
\(\cfrac{x^2+2x+2}{x+1}=\cfrac{(x+1)^2+1}{x+1}=(x+1)+\cfrac{1}{x+1}\);
\(\cfrac{x^2+3x+3}{x+1}=\cfrac{(x^2+3x+2)+1}{x+1}\)\(=\cfrac{(x+2)(x+1)+1}{x+1}\)
\(=x+2+\cfrac{1}{x+1}\)\(=(x+1)+\cfrac{1}{x+1}+1\)
\(\cfrac{x^2+2x}{x+1}=(x+1)-\cfrac{1}{x+1}\);
\(\cfrac{x+1}{x^2+3x+3}=\cfrac{1}{\cfrac{x^2+3x+3}{x+1}}\);
\(\begin{align*} g(t)=\cfrac{1+t^2}{1+2\sqrt{2}t}&=\cfrac{\cfrac{1}{8}(2\sqrt{2}t+1)^2-\cfrac{\sqrt{2}}{2}t-\cfrac{1}{8}+1}{2\sqrt{2}t+1} \\&=\cfrac{\cfrac{1}{8}(2\sqrt{2}t+1)^2-\cfrac{1}{4}(2\sqrt{2}t+1)+\cfrac{9}{8}}{2\sqrt{2}t+1}\\&=\cfrac{1}{8}(2\sqrt{2}t+1)+\cfrac{9}{8(2\sqrt{2}t+1)}-\cfrac{1}{4} \\& \ge 2\sqrt{\cfrac{1}{8}\cdot \cfrac{9}{8}}-\cfrac{1}{4}=2\cdot\cfrac{3}{8}-\cfrac{1}{4}=\cfrac{1}{2}\end{align*}\),
当且仅当\(\cfrac{1}{8}(2\sqrt{2}t+1)=\cfrac{9}{8(2\sqrt{2}t+1)}\),即\(t=\cfrac{\sqrt{2}}{2}\)时取到等号。(这是配凑法,怎么,够震撼吧!)
\(\begin{align*}g(t)=\cfrac{1+t^2}{1+2\sqrt{2}t}&=\cfrac{1+\cfrac{(m-1)^2}{8}}{m}\\&=\cfrac{1}{m}+\cfrac{m^2-2m+1}{8m}\\&=\cfrac{1}{m}+\cfrac{m}{8}-\cfrac{1}{4}+\cfrac{1}{8m}\\&=\cfrac{m}{8}+\cfrac{9}{8m}-\cfrac{1}{4}\\&=\cfrac{1+2\sqrt{2}t}{8}+\cfrac{9}{8(1+2\sqrt{2}t)}-\cfrac{1}{4} \\& \ge 2\sqrt{\cfrac{1}{8}\cdot \cfrac{9}{8}}-\cfrac{1}{4}=2\cdot\cfrac{3}{8}-\cfrac{1}{4}=\cfrac{1}{2}\end{align*}\),
当且仅当\(\cfrac{1}{8}(2\sqrt{2}t+1)=\cfrac{9}{8(2\sqrt{2}t+1)}\),即\(t=\cfrac{\sqrt{2}}{2}\)时取到等号。
反思总结:一般碰到分式形式的一元或二元函数,其特点是分子分母的最高次是2倍关系;我们常常将其转化为部分分式的形式,这样就能用均值不等式或对号函数的单调性来解决问题了。
相关链接
1、分式型函数相关知识 ;
2、变量集中 ;

 变换作图中的常用模板函数
变换作图中的常用模板函数

